Logic Behind GST Identification Numbers

Implementation of the Goods and Services Tax (GST) is a crucial reform in the Indian economy. Such a comprehensive overhaul of the tax assessment and reporting systems has not taken place anytime in the country’s economic history. Its impact on the economy is thought to be second only to the liberalization and globalization initiatives in 1991.

Every tax payer in GST is given a 15-digit GST identification number (GSTIN). We will now look at the logic behind each of the numbers. And, it is even possible to correctly surmise a firm’s GSTIN with very few inputs.

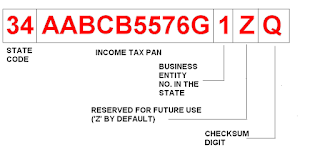
A typical GST number will be like this. Small case and upper case letters are interchangeable.

Digits 1 and 2

The first two digits are the state code in which the company is registered. These codes are taken from Indian Census Data 2011. Every state and union territory has a two-digit unique code. The codes can be obtained from this link http://censusindia.gov.in/Census_Data_2001/PLCN/plcn.html

In the above example, 34 is the code for Pondicherry

Digits 3 to 12

These 10 digits are the company’s Income Tax Permanent Account Number (PAN).

In the above example, AABCB5576G is the PAN of Bharat Sanchar Nigam Ltd (BSNL)

Digit 13

This number is based on the number of registrations of a company in a state for different business purposes, if any. This will be an alphanumeric character. Up to 9 registrations, 1 to 9 is given. When the 10^th registration is made, ‘A’ is allocated. This can go on up to ‘Z’ in which case there will be 35 registrations in the state for the same PAN. 35 is the maximum number of registrations possible for a firm on the same PAN in a state.

In the above case, this is BSNL’s first registration in Pondicherry

Digit 14

This digit is reserved for future use and is currently filled with ‘Z’

Digit 15

This is the trickiest digit of all the fifteen! It is a checksum calculated on the values of the first fourteen digits.

Before explaining the details of manually calculating the checksum, see the following diagram showing the character array and corresponding values.

Take the first character in the example, which is ‘3’. The place value of ‘3’ in the character array is 3 itself. Multiply it by a factor, which is 1 for all odd digits in the GSTIN (that is, for digits 1, 3, 5, 7, 9, 11 and 13) and is 2 for all even digits (digits 2, 4, 6, 8, 10, 12 and 14). Multiplying the factor, we get 3 itself (that is, 3 x 1). Divide it by 36 and see what is the quotient. Leave out the remainder. In this case, this will be 0/36, which is 0 itself. Let’s call this step 1. Again divide the multiplied value by 36 and see what is the remainder (3 in this case). Let’s call this step 2 and add the numbers obtained in steps 1 and 2, which is 0+3 = 3. Let’s keep this number aside as step a1.

Repeat this for the second digit ‘4’. Here, being the second digit, factor is ‘2’. Multiplying the factor, we get 8 (that is, 4 x 2). Divide it by 36 and see what is the quotient. Leave out the remainder. In this case, this will be 8/36, which is 0 itself. Let’s call this step 1. Again divide the multiplied value by 36 and see what is the remainder (8 in this case). Let’s call this step 2 and add the numbers obtained in steps 1 and 2, which is 0+8 = 8. Let’s keep this number aside as step a2.

Third character is ‘A’. Place value is 10. Factor is 1. In Step 1, we get 0, and step 2 we get 10 itself. Adding step 1 and 2, we get 10. Let’s keep this as step a3.

Fourth character is ‘A’. Place value is 10. Factor is 2. Multiplied value is 10x2=20. In Step 1, we get 0, and step 2 we get 20 itself. Adding step 1 and 2, we get 20. Let’s keep this as step a4.

Fifth character is ‘B’. Place value is 11, Factor is 1. We get 11 as step a5.

Sixth character is ‘C’. Place value is 12, Factor is 2. We get 24 as step a6.

Seventh character is ‘B’. Place value is 11, Factor is 1. We get 11 as step a7.

Eighth character is ‘5’. Place value is 5, Factor is 2. We get 10 as step a8.

Ninth character is ‘5’. Place value is 5, Factor is 1. We get 5 as step a9.

Tenth character is ‘7’. Place value is 7, Factor is 2. We get 14 as step a10.

Eleventh character is ‘6’. Place value is 6, Factor is 1. We get 6 as step a11.

Twelfth character is ‘G’. Place value is 16, Factor is 2. We get 32 as step a12.

Thirteenth character is ‘1’. Place value is 1, Factor is 1. We get 1 as step a13.

Fourteenth character is ‘Z’. Place value is 35. Factor is 2. Multiplied value is 35x2=70. In Step 1, we get 70/36=1 and step 2 we get 34 as remainder. Adding step 1 and 2, we get 35. Let’s keep this as step a14.

Now, add all the numbers obtained in steps a1 to a14 = 3 + 8 + 10 + 20 + 11 + 24 + 11 + 10 + 5 + 14 + 6 + 32 + 1 + 35 = 190. Let’s call this step 15A.

Divide the sum obtained in step 15A by 36 and see what’s the remainder. This is 10, in this case (190/36 gives 10 as remainder). Let’s call this step 15B.

Deduct the number obtained in step 15B from 36. Here, this is 36-10=26. Let’s call this step 15C.

Now, divide the number obtained in 15C with 36 and see what’s the remainder. Dividing 26 by 36, we get 26 itself as remainder.

Look up the character with place value 26 in the character array. It is ‘Q’ and hence it is the checksum digit.

If you think the explanation I gave is cumbersome, see this few lines of code in Java which says the same thing. How elegant and precise is software!

public static String getGSTINWithCheckDigit(String gstinWOCheckDigit) throws Exception {

int factor = 2; int sum = 0;

int checkCodePoint = 0;

char[] cpChars; char[] inputChars;

cpChars = "0123456789ABCDEFGHIJKLMNOPQRSTUVWXYZ";

inputChars= gstinWOCheckDigit.trim().toUpperCase().toCharArray();

int mod = cpChars.length;

   for (int i = inputChars.length - 1; i >= 0; i--) {

   int codePoint = -1;

   for (int j = 0; j < cpChars.length; j++) {

   if (cpChars[j] == inputChars[i]) {

      codePoint = j;

     }}

   int digit = factor * codePoint;

   factor = (factor == 2) ? 1 : 2;

   digit = (digit / mod) + (digit % mod);

   sum += digit;

   }

   checkCodePoint = (mod - (sum % mod)) % mod;

   return gstinWOCheckDigit + cpChars[checkCodePoint];

   }}

By the way, I don’t know Java. My humble and little experience is with VB, but the logic is clearly visible.

As a practice example, try to find out the checksum digit of the following GSTIN (first 14 characters are given).