Implementation of the Goods and
Services Tax (GST) is a crucial reform in the Indian economy. Such a
comprehensive overhaul of the tax assessment and reporting systems has not
taken place anytime in the country’s economic history. Its impact on the
economy is thought to be second only to the liberalization and globalization
initiatives in 1991.
Every tax payer in GST is given a
15-digit GST identification number (GSTIN). We will now look at the logic
behind each of the numbers. And, it is even possible to correctly surmise a
firm’s GSTIN with very few inputs.
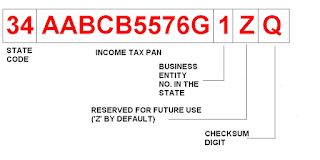
A typical GST number will be like
this. Small case and upper case letters are interchangeable.
Digits 1 and 2
The first two digits are the state
code in which the company is registered. These codes are taken from Indian Census
Data 2011. Every state and union territory has a two-digit unique code. The
codes can be obtained from this link http://censusindia.gov.in/Census_Data_2001/PLCN/plcn.html
In the above example, 34 is the code
for Pondicherry
Digits 3 to 12
These 10 digits are the company’s
Income Tax Permanent Account Number (PAN).
In the above example, AABCB5576G is
the PAN of Bharat Sanchar Nigam Ltd (BSNL)
Digit 13
This number is based on the number of registrations
of a company in a state for different business purposes, if any. This will be
an alphanumeric character. Up to 9 registrations, 1 to 9 is given. When the 10th
registration is made, ‘A’ is allocated. This can go on up to ‘Z’ in which case there
will be 35 registrations in the state for the same PAN. 35 is the maximum
number of registrations possible for a firm on the same PAN in a state.
In the above case, this is BSNL’s
first registration in Pondicherry
Digit 14
This digit is reserved for future use
and is currently filled with ‘Z’
Digit 15
This is the trickiest digit of all the
fifteen! It is a checksum calculated on the values of the first fourteen
digits.
Before explaining the details of manually
calculating the checksum, see the following diagram showing the character array
and corresponding values.
Take the first character in the
example, which is ‘3’. The place value of ‘3’ in the character array is 3
itself. Multiply it by a factor, which is 1 for all odd digits in the GSTIN
(that is, for digits 1, 3, 5, 7, 9, 11 and 13) and is 2 for all even digits
(digits 2, 4, 6, 8, 10, 12 and 14). Multiplying the factor, we get 3 itself
(that is, 3 x 1). Divide it by 36 and see what is the quotient. Leave out the
remainder. In this case, this will be 0/36, which is 0 itself. Let’s call this
step 1. Again divide the multiplied value by 36 and see what is the remainder
(3 in this case). Let’s call this step 2 and add the numbers obtained in steps
1 and 2, which is 0+3 = 3. Let’s keep this number aside as step a1.
Repeat this for the second digit ‘4’.
Here, being the second digit, factor is ‘2’. Multiplying the factor, we get 8
(that is, 4 x 2). Divide it by 36 and see what is the quotient. Leave out the
remainder. In this case, this will be 8/36, which is 0 itself. Let’s call this
step 1. Again divide the multiplied value by 36 and see what is the remainder (8
in this case). Let’s call this step 2 and add the numbers obtained in steps 1
and 2, which is 0+8 = 8. Let’s keep this number aside as step a2.
Third character is ‘A’. Place value is
10. Factor is 1. In Step 1, we get 0, and step 2 we get 10 itself. Adding step
1 and 2, we get 10. Let’s keep this as step a3.
Fourth character is ‘A’. Place value
is 10. Factor is 2. Multiplied value is 10x2=20. In Step 1, we get 0, and step 2
we get 20 itself. Adding step 1 and 2, we get 20. Let’s keep this as step a4.
Fifth character is ‘B’. Place value is
11, Factor is 1. We get 11 as step a5.
Sixth character is ‘C’. Place value is
12, Factor is 2. We get 24 as step a6.
Seventh character is ‘B’. Place value
is 11, Factor is 1. We get 11 as step a7.
Eighth character is ‘5’. Place value
is 5, Factor is 2. We get 10 as step a8.
Ninth character is ‘5’. Place value is
5, Factor is 1. We get 5 as step a9.
Tenth character is ‘7’. Place value is
7, Factor is 2. We get 14 as step a10.
Eleventh character is ‘6’. Place value
is 6, Factor is 1. We get 6 as step a11.
Twelfth character is ‘G’. Place value
is 16, Factor is 2. We get 32 as step a12.
Thirteenth character is ‘1’. Place
value is 1, Factor is 1. We get 1 as step a13.
Fourteenth character is ‘Z’. Place
value is 35. Factor is 2. Multiplied value is 35x2=70. In Step 1, we get
70/36=1 and step 2 we get 34 as remainder. Adding step 1 and 2, we get 35. Let’s
keep this as step a14.
Now, add all the numbers obtained in
steps a1 to a14 = 3 + 8 + 10 + 20 + 11 + 24 + 11 + 10 + 5 + 14 + 6 + 32 + 1 + 35
= 190. Let’s call this step 15A.
Divide the sum obtained in step 15A by
36 and see what’s the remainder. This is 10, in this case (190/36 gives 10 as
remainder). Let’s call this step 15B.
Deduct the number obtained in step 15B
from 36. Here, this is 36-10=26. Let’s call this step 15C.
Now, divide the number obtained in 15C
with 36 and see what’s the remainder. Dividing 26 by 36, we get 26 itself as
remainder.
Look up the character with place value
26 in the character array. It is ‘Q’ and hence it is the checksum digit.
If you think the explanation I gave is
cumbersome, see this few lines of code in Java which says the same thing. How
elegant and precise is software!
public
static String getGSTINWithCheckDigit(String gstinWOCheckDigit) throws Exception
{
int factor = 2; int sum = 0;
int checkCodePoint = 0;
char[] cpChars; char[] inputChars;
cpChars = "0123456789ABCDEFGHIJKLMNOPQRSTUVWXYZ";
inputChars= gstinWOCheckDigit.trim().toUpperCase().toCharArray();
int mod = cpChars.length;
for (int i = inputChars.length - 1; i >= 0; i--) {
int codePoint = -1;
for (int j = 0; j <
cpChars.length; j++) {
if (cpChars[j] ==
inputChars[i]) {
codePoint =
j;
}}
int digit = factor *
codePoint;
factor = (factor == 2) ?
1 : 2;
digit = (digit / mod) +
(digit % mod);
sum += digit;
}
checkCodePoint = (mod - (sum %
mod)) % mod;
return gstinWOCheckDigit +
cpChars[checkCodePoint];
}}
By the way, I don’t know Java. My
humble and little experience is with VB, but the logic is clearly visible.
As a practice example, try to find out
the checksum digit of the following GSTIN (first 14 characters are given).